User Guide

Block Objects

Basic uniform blocks

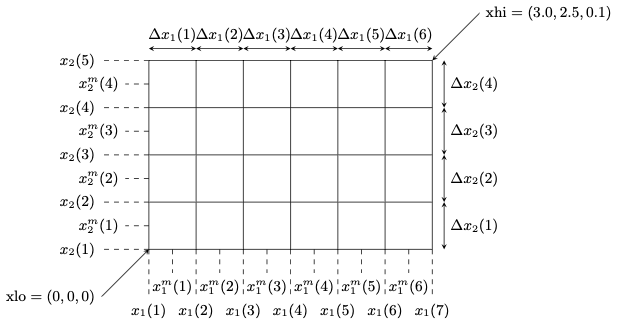
LEAP uses structured Cartesian blocks. The derived type block_obj defines a standard 3-dimensional LEAP block of size $n_1\times n_2\times n_3$ , where $n_d$ is the number of cells along the $x_d$ -axis . For example a $6\times 5\times 1$ block, with corner values $\mathrm{xlo}=(0,0,0)$ and $\mathrm{xhi}=(3.0,2.5,0.1)$ looks like this

use leapKinds
use leapBlock
type(block_obj) :: myblock

! The following code defines the block above
call myblock%Initialize(ngc=0,parallel)
call myblock%SetupUniformGrid(xlo=[0.0_wp,0.0_wp,0.0_wp], &
                              xhi=[3.0,2.5,0.1],          &
                              lo =[1,1,1],                &
                              hi =[6,5,1])

For each direction $d=1, 2,3$ , we define the nodal positions $x_d(i)$ (for $i=1,n_d+1$ ), mid-point positions $x_d^m(i)=(x_d(i)+x_d(i+1))/2$ (for $i=1,n_d$ ), and spacing $\Delta x(i)=x(i+1)-x(i)$ (for $i=1,n_d$ ). Thus, for a given block cell $(i,j,k)$ , we have the following information.

integer         :: i,j

! Display the grid information for cell i=3,j=2
i = 3; j = 2
print*, "x1(i)=",  myblock%axis(1)%x(i)
print*, "x1m(i)=", myblock%axis(1)%xm(i)
print*, "dx1(i)=", myblock%axis(1)%dxm(i)

print*, "x2(j)=",  myblock%axis(2)%x(j)
print*, "x2m(j)=", myblock%axis(2)%xm(j)
print*, "dx2(j)=", myblock%axis(2)%dxm(j)

! You may also get this information from the convenience pointers
print*, "x1(i)=",  myblock%x(i)
print*, "x1m(i)=", myblock%xm(i)
print*, "dx1(i)=", myblock%dxm(i)

print*, "x2(j)=",  myblock%y(j)
print*, "x2m(j)=", myblock%ym(j)
print*, "dx2(j)=", myblock%yxm(j)

Ghost cells and periodicity

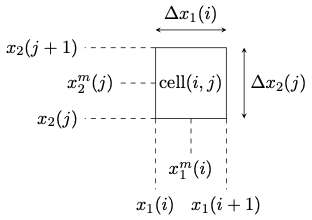
Ghost cells may be added to blocks to help perform computations in parallel. Use the parameter ngc to specify how many ghost cells are needed. With the example above, setting ngc=2, creates a block like this:

use leapKinds
use leapBlock
type(block_obj) :: myblock

! Create a block with 2 ghostcells
call myblock%Initialize(ngc=2,parallel)
call myblock%SetupUniformGrid(xlo=[0.0_wp,0.0_wp,0.0_wp], &
                              xhi=[3.0,2.5,0.1],          &
                              lo =[1,1,1],                &
                              hi =[6,5,1])

The axis positions in the ghost cells depend on the domain periodicity. By default, all directions are non-periodic. However, this can be changed as follows.

use leapKinds
use leapBlock
type(block_obj) :: myblock

! Define a block with the third direction periodic
call myblock%Initialize(ngc=2,parallel)
call myblock%SetPeriodicity([.false.,.false.,.true.])
call myblock%SetupUniformGrid(xlo=[0.0_wp,0.0_wp,0.0_wp], &
                              xhi=[3.0,2.5,0.1],          &
                              lo =[1,1,1],                &
                              hi =[6,5,1])

to set periodicity in the $x_3$ -direction only. Since the $x_1$ -direction is non-periodic, LEAP will determine $x_1(0)$ and $x_1(-1)$ in the example above as follows $\begin{eqnarray*} \Delta x_1(1) &=& x_1(2)-x_1(1)\\ x_1(0)&=& x_1(1)-1\times\Delta x_1(1)\\ x_1(-1)&=& x_1(1)-2\times\Delta x_1(1) \end{eqnarray*}$ The same happens on the other end of the $x_1$ -direction $\begin{eqnarray*} \Delta x(n_1) &=& x_1(n_1)-x_1(n_1+1)\\ x_1(n_1+2)&=& x_1(n_1+1)+1\times\Delta x_1(n_1)\\ x_1(n_1+3)&=& x_1(n_1+1)+2\times\Delta x_1(n_1) \end{eqnarray*}$

Now, let's consider the periodic direction $x_3$ . LEAP will define the positions in the ghost cells based on the following $\begin{eqnarray*} x_3(0)&=& x_3(1)-\Delta x_3(n_3)\\ x_3(-1)&=& x_3(1)-\Delta x_3(n_3)-\Delta x_3(n_3-1)\\ x_3(n_3+2)&=& x_3(n_3+1)+\Delta x_3(1)\\ x_3(n_3+3)&=& x_3(n_3+1)+\Delta x_3(1)+\Delta x_3(2) \end{eqnarray*}$

Pseudo-2D blocks

You may create ``pseudo-2D'' blocks by making one of the directions periodic and specifying only one grid point in that direction. The example above is pseudo-2D since $n_3=1$ and the $x_3$ -direction is periodic. The domain has a non-zero thickness in the $x_3$ -direction, however, no variations can be resolved in this direction.

Due to how Fortran loops over multidimensional arrays, it is recommended that the pseudo-2D configurations use the $x_3$ -direction as the periodic direction with $n_3=1$ .

Non-uniform blocks

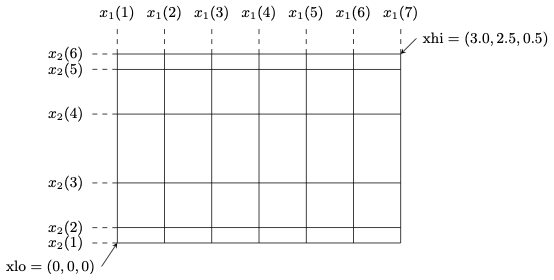
The following example creates a rectangular grid with vertical stretching that concentrates points at the top and bottom boundaries. The result looks like this:

Further information on the subroutines below can be found in src/kernel/leapblock.f90.

use leapKinds
use leapBlock
type(block_obj) :: myblock
real(wp)        :: xlo, xhi
integer         :: N(3)
real(wp)        :: r
integer         :: dir
integer         :: i,j,k

! Set the stretching factor
r = 1.8_wp

! Define domain extents
xlo = [0.0_wp, 0.0_wp, 0.0_wp]
xhi = [3.0_wp, 2.5_wp, 0.5_wp]

! Define a block that is non-periodic in the x2-direction only
call myblock%Initialize(ngc=2,parallel)
call myblock%SetPeriodicity([.true.,.false.,.true.])

! Set grid size
myblock%lo  = [1,1,1]
myblock%hi  = [6,5,1]

! Number of grid points in each direction
N = myblock%hi-myblock%lo + 1

! Initialize each axis manually
do dir=1,3
  call myblock%axis(dir)%Initialize(myblock%lo(dir),   &
                                    myblock%hi(dir),   &
                                    myblock%ngc)
end do

! Link points x(:) to axis(1)%x(:), y(:) to axis(2)%x(:), etc
call myblock%SetConveniencePointers()

! Make x- and z- axes uniform
do k=myblock%lo(3),myblock%hi(3)+1
  z(k) = xlo(3) + (k-myblock%lo(3))/real(N(3),wp)*(xhi(3)-xlo(3))
end do
do i=myblock%lo(1),myblock%hi(1)+1
  x(i) = xlo(1) + (i-myblock%lo(1))/real(N(1),wp)*(xhi(1)-xlo(1))
end do

! Make y-axis stretched
do j=myblock%lo(2),myblock%hi(2)+1
  ! Uniform position
  y(j) = xlo(2) + (j-myblock%lo(2))/real(N(2),wp)*(xhi(2)-xlo(2))
  ! Stretched position
  y(j) = 0.5_wp*(xhi(2)+xlo(2)) + 0.5_wp*(xhi(2)-xlo(2))*   &
         tanh(r*(y(j)-0.5_wp*(xhi(2)+xlo(2))/( 0.5_wp*(xhi(2)-xlo(2)) )/tanh(r)
end do

! Update values within ghostcells
call myblock%UpdateGridGhostCells()

! Update midpoints (xm, ym, zm)
call myblock%UpdateMidPoints()

! Update spacing (dxm)
call myblock%UpdateSpacing()

! Create MPI Type for ghostcell communication (needed even in serial runs)
call myblock%SetupMPITypes()

Parallel partitioned blocks

For parallel runs, it useful to decompose the domain across multiple MPI ranks. Each rank will handle the computation on its subdomain, and communicate with neighboring ranks when needed.

Partitionning a domain in LEAP is simple. The recommended approach is to define a global block first, then let LEAP partition it and handle the MPI rank mapping. With the example above, partitionning the domain with 2 ranks in the $x_1$ -direction, 2 ranks in the $x_2$ -direction, and 1 rank in the $x_1$ -direction yields the following subdivision:

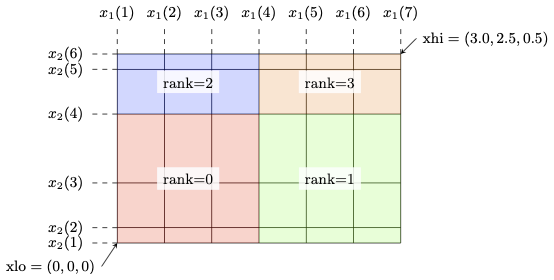
The code to do this is the following:

use leapKinds
use leapBlock
type(block_obj) :: myblock
real(wp)        :: xlo, xhi
integer         :: N(3)
integer         :: Nb(3)
real(wp)        :: r
integer         :: dir
integer         :: i,j,k

! Number of MPI ranks in each direction
Nb(3) = [2, 2, 1]

! Set the stretching factor
r = 1.8_wp

! Define domain extents
xlo = [0.0_wp, 0.0_wp, 0.0_wp]
xhi = [3.0_wp, 2.5_wp, 0.5_wp]

! Define a block that is non-periodic in the x2-direction only
call myblock%Initialize(ngc=2,parallel)
call myblock%SetPeriodicity([.true.,.false.,.true.])

! Set grid size
myblock%lo  = [1,1,1]
myblock%hi  = [6,5,1]

! Number of grid points in each direction
N = myblock%hi-myblock%lo + 1

! Initialize each axis manually
do dir=1,3
  call myblock%axis(dir)%Initialize(myblock%lo(dir),   &
                                    myblock%hi(dir),   &
                                    myblock%ngc)
end do

! Link points x(:) to axis(1)%x(:), y(:) to axis(2)%x(:), etc
call myblock%SetConveniencePointers()

! Make x- and z- axes uniform
do k=myblock%lo(3),myblock%hi(3)+1
  z(k) = xlo(3) + (k-myblock%lo(3))/real(N(3),wp)*(xhi(3)-xlo(3))
end do
do i=myblock%lo(1),myblock%hi(1)+1
  x(i) = xlo(1) + (i-myblock%lo(1))/real(N(1),wp)*(xhi(1)-xlo(1))
end do

! Make y-axis stretched
do j=myblock%lo(2),myblock%hi(2)+1
  ! Uniform position
  y(j) = xlo(2) + (j-myblock%lo(2))/real(N(2),wp)*(xhi(2)-xlo(2))
  ! Stretched position
  y(j) = 0.5_wp*(xhi(2)+xlo(2)) + 0.5_wp*(xhi(2)-xlo(2))*   &
         tanh(r*(y(j)-0.5_wp*(xhi(2)+xlo(2))/( 0.5_wp*(xhi(2)-xlo(2)) )/tanh(r)
end do

! Partition block (this will also update the midpoints, spacing, and MPI types)
call myblock%Partition(Nb)

Using multiple blocks

In LEAP, you are not restricted to having only 1 block. You may instantiate multiple blocks to define different grids, whether they are overlapping or not. For example, one may define two completely overlapping grids: a uniform grid of size $16\times 8\times 1$ and stretched grid of size $32\times 16\times 1$ as pictured below. You can also have partially overlapping, or non-overlapping grids

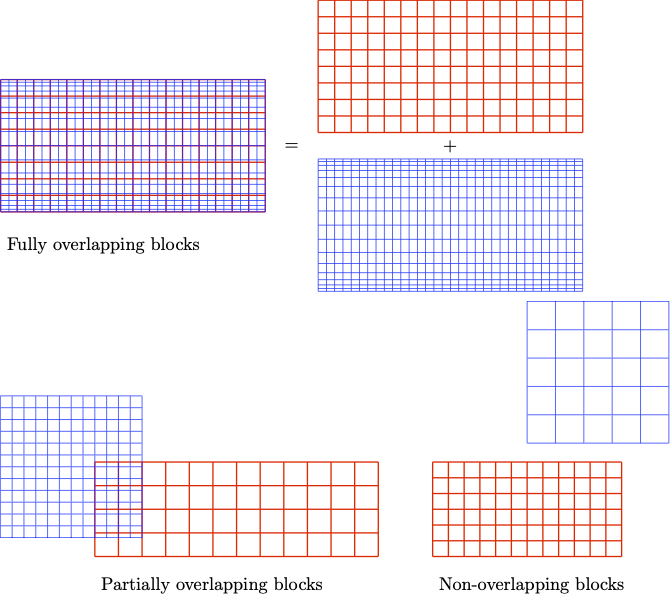
Writing/Reading blocks

Writing block information to file is fairly straightforward.

call myblock%Write('block.hdf5')

This will write an HDF5 file that contains all necessary information to regenerate the block. You may also read from file using:

call myblock%Read('block.hdf5')